INTRODUCTION
Recently, network analyses for fMRI data have emerged that characterize the functional relationships between brain regions. A typical neuroimaging network analysis involves defining brain regions (nodes), quantifying a measure of association between all pairs of brain regions (edges) to produce a connectivity matrix, thresholding these associations to obtain a more sparse connectivity matrix, and then calculating summary statistics that reflect properties of the network. Network summaries include metrics that reflect local or global communication ability (e.g., clustering coefficient, path length, and efficiency), centrality metrics (e.g., betweenness, closeness, and eigenvector centrality), and community structure (e.g., small-worldness).
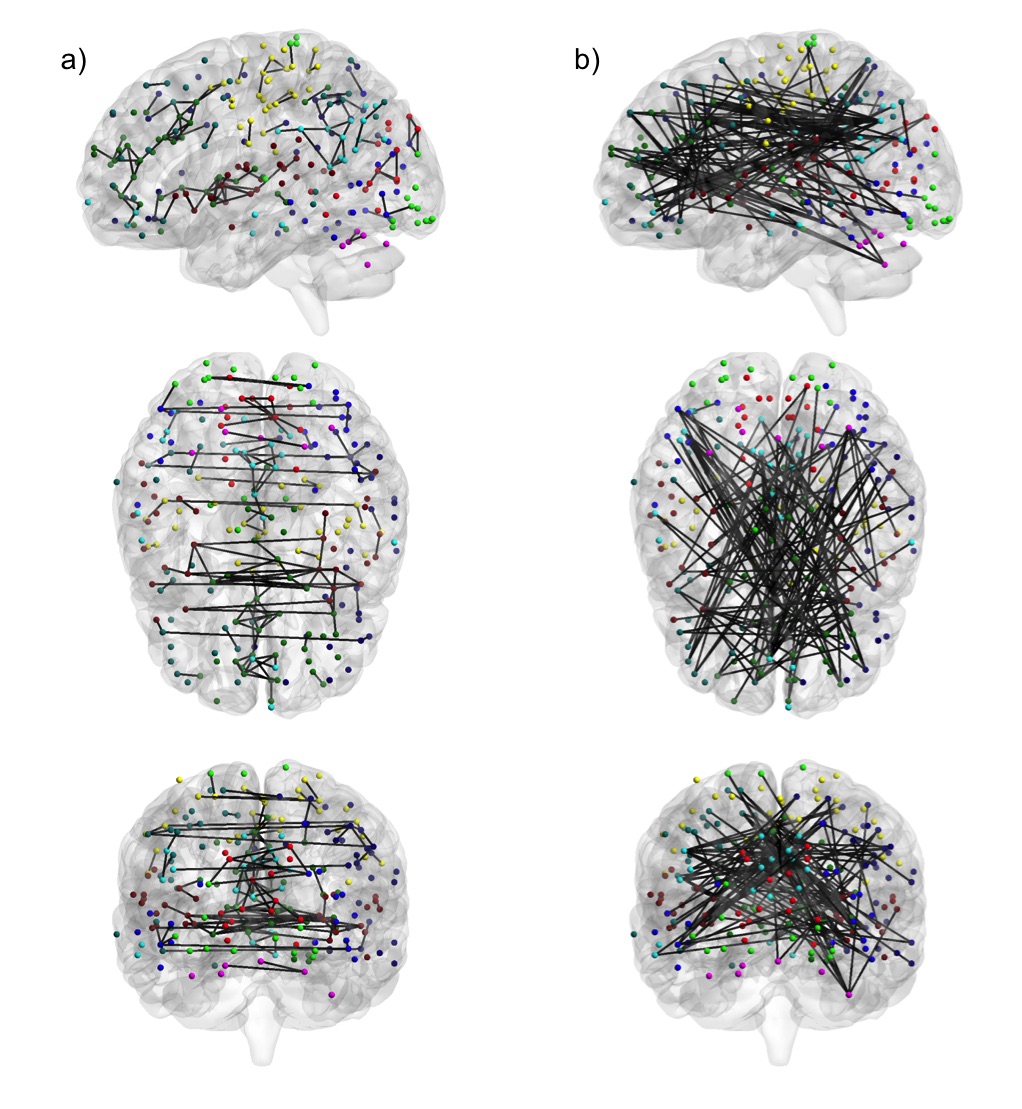
Functional connectivity (FC) is commonly measured by correlation, but this reflects the marginal association between two nodes, which could be mediated by connections to a third-party node. Partial correlation, however, measures direct FC by calculating correlation after regressing out the effects from all other nodes. We have developed a Dens-based method that allows fast and reliable computation of the partial correlation matrix, at a specified network sparsity level (Wang et al., 2016). We are also currently developing methods for network estimation via graphical models, as well as dynamic FC methods that measure the change in functional networks over time.
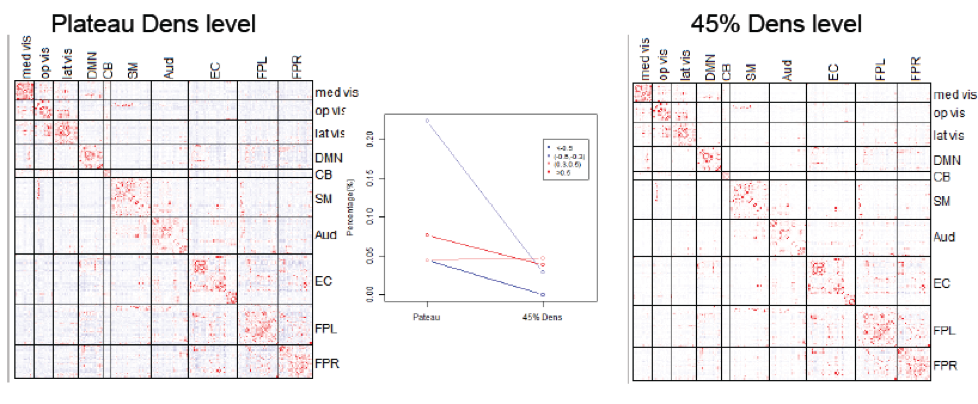
Functional connectivity (FC) is commonly measured by correlation, but this reflects the marginal association between two nodes, which could be mediated by connections to a third-party node. Partial correlation, however, measures direct FC by calculating correlation after regressing out the effects from all other nodes. We have developed a Dens-based method that allows fast and reliable computation of the partial correlation matrix, at a specified network sparsity level (Wang et al., 2016). We are also currently developing methods for network estimation via graphical models, as well as dynamic FC methods that measure the change in functional networks over time.
REFERENCES
Wang, Y., Kang, J., Kemmer, P.B., & Guo, Y. (2016) An efficient and reliable statistical method for estimating functional connectivity in large scale brain networks using partial correlation. Frontiers in Neuroscience. In press.
Xue, W., Bowman, F. D., Pileggi, A. V., & Mayer, A. R. (2015). A multimodal approach for determining brain networks by jointly modeling functional and structural connectivity. Frontiers in computational neuroscience, 9.
Kemmer, P. B., Guo, Y., Wang, Y., & Pagnoni, G. (2015). Network-based characterization of brain functional connectivity in Zen practitioners. Frontiers in psychology, 6.