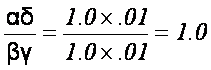7 Aug 2002 – DRAFT – some issues that need to be resolved are highlighted; please provide comments/suggestions to Kevin Sullivan (cdckms@sph.emory.edu); Copyright © 2001 Data Description Inc.

LESSON 8

SELECTION BIAS

8-1 Selection Bias

Selection bias - systematic error in how subjects are selected into a study or loss of subjects

Selection Bias in Different Study Designs

Examples of selection bias provided –

· Case-control example – L-tryptophan and EMS, publicity may have increased likelihood that those taking L-tryptophan would be diagnosed/reported

· Clinical trial example – loss to follow-up differs in one treatment group compared to another

· Cross-sectional example – selective survival

Example of Selection Bias in Cohort Studies

· The primary sources of such selection bias are loss-to-follow-up, withdrawal or non-response.

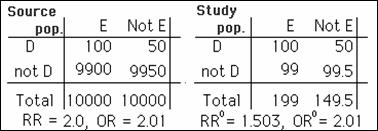
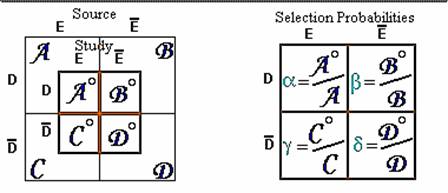
Consider table that describes the five-year follow-up for disease in a population.

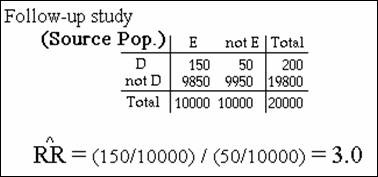
10% random sample from this population:

RR = 3.0; no bias

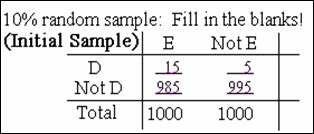
Assume initial cohort obtained from 10% sampling. However:

· 20% of exposed persons lost to follow-up

· 10% of unexposed persons are lost

· assume lost to follow-up not affected by disease status

RR = 3; no bias

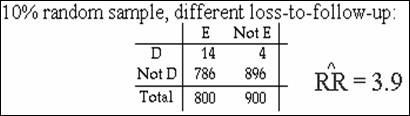
Suppose that a different pattern of loss-to follow-up results in the two-way table shown here.

Other Examples

v Selection bias – so-called “healthy worker effect” - workers tend to be healthier than general population.

v Selection bias - using volunteers, may have different characteristics from persons who do not volunteer.

v Clinic-based studies frequently suffer from selection bias because their patients tend to have more severe illness than persons in a population-based sample.

8-2 Selection Bias (continued)

Selection Ratios and Selection Probabilities

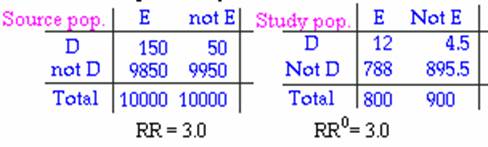
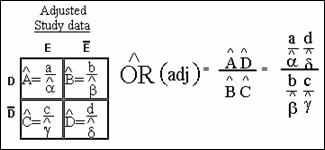
1. What are alpha, beta, gamma, and delta for these data?

alpha α = 12/150 = .08

beta β = 4.5/50 = .09

gamma γ = 88/9850 = .08

delta δ = 895.5/9950 = .09

Selection Probabilities

	E
D	α= 12/150 = .08	β= .09
	γ= .08	δ=.09

2. Is there selection bias in either the odds ratio or the risk ratio?

No

3. Cross-product of selection probabilities?

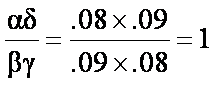
OR=3.03 =4.00

	E
D	α= .093	β= .08
	γ= .08	δ=.09

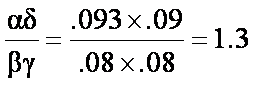
Why is this important? Need to think about these probabilities in a study and how they would impact the results.

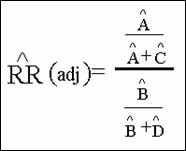
Quantitative Assessment of Selection Bias

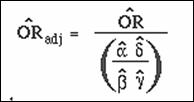
Selection bias and the odds ratio.

Estimate of is biased when study population OR^o is meaningfully different from source population OR.

Rule for assessing selection bias in the odds ratio

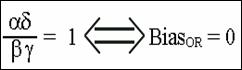
The bias is either > 0, = 0, or < 0 depending on whether the cross product ratio of selection probabilities is > 1, = 1, or < 1.

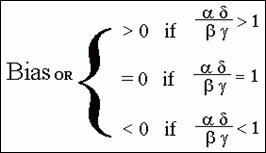
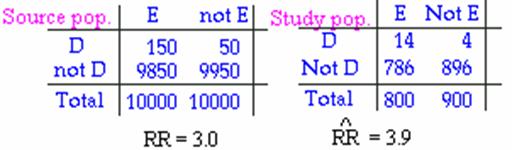
Selection Bias for Risk Ratio

The cross-product of selection ratios [(αδ)/(βγ)] used for the OR can be used to assess bias for the RR when disease is rare.

Works fine in this example:

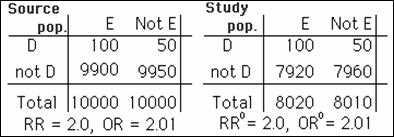
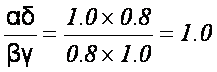
Not so well in this example:

Some examples of Selection given for Case-Control, Cohort, and Cross-Sectional studies

8-4 Selection Bias (continued)

What Can Be Done About Selection Bias Quantitatively?

Let’s not worry about the math in this section.

If selection probabilities or ratio of certain selection probabilities can be estimate, it is possible to calculate an “adjusted” or “corrected” odds ratio and/or risk ratio.

What Can Be Done About Selection Bias Qualitatively?

Selection probabilities usually not known

Prevent/minimize selection bias when designing study

Case-control studies – select controls representative of source that produced cases is an important issue. Some may select 2 or more control groups.

To minimize selection bias in case-control studies:

Use incident cases (rather than prevalent)

Use population-based design rather than hospital-based

To minimize selection bias in cohort studies

High response

Minimize loss-to-follow-up

In Discussion section of manuscript, address possible selection bias