7 Aug  2002 – DRAFT – some issues that may need to be resolved are highlighted; please provide comments/suggestions to Kevin Sullivan (cdckms@sph.emory.edu); Copyright © 2001 Data Description Inc.

 

LESSON   13    

Options for controlling for confounders

 

Design options

          Randomization

RCT only

Groups are similar (on both measured and unmeasured factors)

          Restriction

                   Easy, inexpensive

                   Generalizability

          Matching – most freq with case-control studies

                   Gain precision

                   Number of controls per case

                   Matched analyses

 

Analysis options

          Stratified analysis

          Mathematical modeling

 

 

Mathematical Modeling

 

Introduction to Mathematical Modeling

 

A mathematical model is a mathematical expression that describes how an outcome variable can be predicted from explanatory variables.

 

 

 

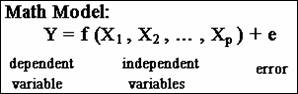
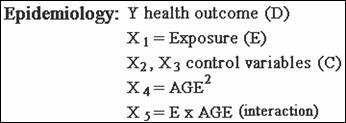
Linear regression – usually a continuous outcome variable (e.g., blood pressure, antibody level, weight); predictor variables can be categorical or continuous.

 

The Logistic Model

 

In epidemiology many times the outcome variable is dichotomous. When the dependent variable is dichotomous, the most popular mathematical model is a non-linear model called the logistic model.

 

 

 

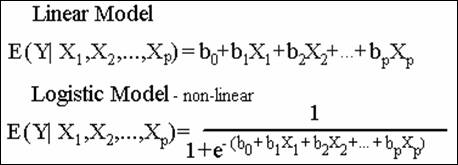
Table 14-2.  Example Data 1: Hypothetical cohort study of the relationship between smoking and coronary heart disease (CHD) stratified on sex

 

Females

 

Smoker

Non-Smoker

 

CHD

5

8

13

No CHD

45

142

187

 

50

150

200

Risk

10.0%

5.3%

 

Odds Ratio for females (ORf) = 2.0 (0.6, 6.3)

 

Males

 

Smoker

Non-Smoker

 

CHD

300

50

350

No CHD

300

150

450

 

600

200

800

Risk

50.0%

25.0%

 

Odds Ratio for males (ORm) = 3.0 (2.1, 4.3)

----

Summary information

Directly adjusted OR = 2.9 (2.1, 4.1)

Mantel-Haenszel OR = 2.9 (2.1, 4.1)

 

 

Chi-square p-value (MH) p-value < .001

 

 

 

Table 14-9.  Example data 1: Hypothetical cohort study of the relationship between smoking and coronary heart disease (CHD) controlling for the sex of the individual, logistic regression model

 

 

There were  363 type  1.0's  (model gives log odds of this type) and 637 type   .0's.

 

Log likelihood   = -575.0730

Likelihood ratio =  158.1036 2 df  (P = .0000)

 

Dependent Variable =        CHD

 

                        Standard

            Coefficient  Error    Coef/SE "P value"

CONSTANT   -3.0336       .2997    -10.1211  .0000

SMOKE       1.0618       .1733      6.1277  .0000

SEX         1.9643       .3045      6.4505  .0000

 

                   95.0-% confidence limits

            Coefficient             Odds ratio

        lower           upper  lower           upper

        limit           limit  limit           limit

SMOKE   .7222  1.0618  1.4015 2.0590  2.8916  4.0611

SEX    1.3675  1.9643  2.5612 3.9254  7.1302 12.9513

 

TABLE 14-14.  Advantages and disadvantages of stratification and logistic regression.

 

 

Stratification

Logistic Regression

Parameters estimated

RR, RD, OR, IDR, IDD, others

OR

Validity of parameters estimated

More valid (no model assumptions)

Less valid (based on model assumptions)

Exposure and third variables

Must be categorical

Can be categorical or continuous

Number of third variables or categories in third variables

Compared to logistic regression, limited

Compared to stratified analysis, can usually have many more variables or variables with many categories