LESSON 11
![]()
CONFOUNDING
INVOLVING SEVERAL RISK FACTORS
Issue: how do deal with several risk factors that
may confound an E→D relationship
Assumption: no risk factors are effect modifiers
Two Fundamental Principles for Confounding with Two
or More Risk Factors
1. Joint
control of 2+ variables may give different results from controlling each
variable separately. The adjusted
estimate that controls for all risk factors is the “standard” for which
conclusions of confounding are based.
2. Not
all variables may need to be controlled.
Data-based joint confounding – meaningful difference
between crude and adjusted effect when controlling for all
potential confounders
aRR(age, smoking) = 2.4
cRR = 1.5
Data-based
marginal confounding – meaningful difference between crude and adjusted effect controlling
for only one confounder
cRR = 1.5 aRR(age) = 1.5
aRR(smoking)
= 2.4
Considering
principle 2, an adjusted estimate for a subset of risk factors may adequately
control for confounding.
Example:
cRR = 2; aRR(K, L) = 1.0; aRR(K) = 1.0; aRR(L) = 1.0
Why
not always control for all potential confounders? Validity vs. Precision
Confounding:
Validity versus Precision

Identifying a subset of confounders giving a precise estimate
(yet still “valid”) is important enough to make such examination worthwhile.
Study Questions (Q11.7)
A clinical trial to determine effectiveness of a treatment.
1. The cRR =
6.28 and the aRR(AGE, SERH, TSZ, INSG) = 8.24.
Confounding?
Four subsets shown below.
2. What
criteria may we use to reduce the number of candidate subsets? Note the answer there is +/- 10% around adjusted
estimate.
Below are the results from the gold standard and the 4
candidate subsets whose aRR is within 10% of the gold standard:
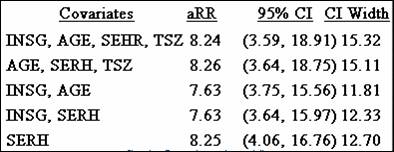
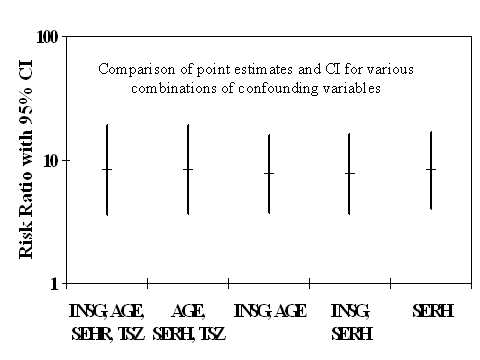
3. The most
valid estimate results from controlling which covariates?
4. The most
precise estimate results from controlling which covariates?
5. Which
covariates do you think are most appropriate to control?
A valid estimate of effect is most important.
Consider the trade-off between controlling for enough risk
factors to maintain validity and loss in precision from control of too many
variables.
Study Designs by Bias
Comparison of study designs for assessing exposure-disease
relationships
Strongest Weakest
Clinical Trial
Cohort Case-Control Cross-Sectional
|--------------------------|-------------------------|-------------------------|
Systematic Error
Selection
Bias
√ √√ √√√
√√√
Loss to Follow-up Berkson’s Survival
Information
Bias
√ √ √√√
√√√
E→D E→D E←D
E↔D
Recall Self-report
Confounding
Unlikely √√ √√ √√
Note: Sampling Error
Affects all designs; can reduce by
increasing sample size