LESSON 10
![]()
CONFOUNDING
10-1 Concept
and Definition
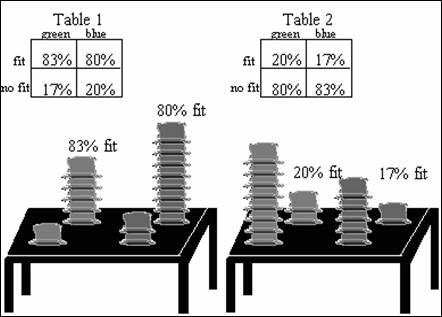
Simpson's Paradox is illustrated by a hat shopping
Confounding – a bias that may occur when there is failure to account for other
variables, like age, gender, or smoking status, in assessing E→D
relationships.
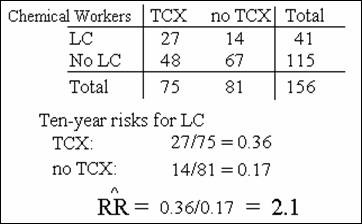
Example: Relationship between TCX and Lung Cancer
More
smokers among those exposed to TCX than those unexposed to TCX?
“Stratify” on smoking history.
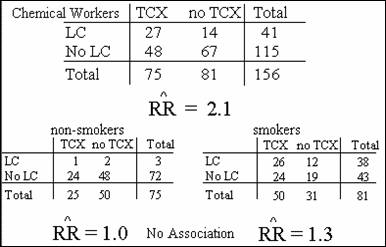
In this example, we are controlling for smoking history.
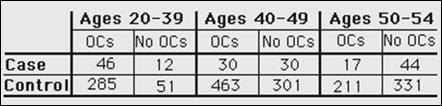
A study finds that alcohol consumption is associated
with lung cancer, crude OR = 3.5. Using the data below, determine whether
smoking could be confounding this relationship.
1.
What is the OR among smokers? . . . ???
2.
What is the OR among non-smokers? . . ???
3.
Does the OR change when we control for smoking status?
???
4.
Is there evidence from this data that smoking is a
confounder of the relationship between alcohol consumption and lung cancer? ???
Confounding assessed by comparing crude estimate of effect (e.g.,
![]() ) where no variables are controlled, with adjusted
estimate of effect (e.g.,
) where no variables are controlled, with adjusted
estimate of effect (e.g., ![]() ), where one or more variables are controlled.
), where one or more variables are controlled.
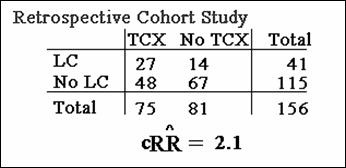
From TCX->Lung cancer example:
![]() = 2.1
= 2.1
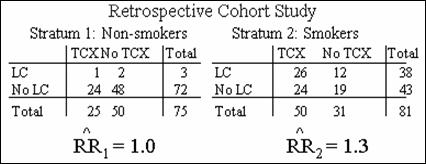
![]() = ? Must be between two stratum-specific
estimates 1.0 & 1.3
= ? Must be between two stratum-specific
estimates 1.0 & 1.3
Note: We will discuss how to calculate an adjusted value later.
How do we decide if there is confounding?
The data-based criterion for confounding:
Crude estimate is meaningfully different
from adjusted estimate
How different must these two
estimates be to conclude there is confounding?
The investigator must decide whether or not there is an “important”
difference.

No statistical test for confounding
Common approach - prior to
looking at data, determine change of crude compared to adjusted estimate,
typically 10 per cent.
Example: crude risk ratio = 4, a 10% change; if adjusted risk ratio were
below 3.6 or above 4.4 we would say that confounding has occurred.

10-2 Adjusted
Estimates
Example: TCX and Lung Cancer.
What is a “crude” estimate?
How to derive “adjusted” estimate?
Combine stratum specific estimates to obtain a single summary
measure; a weighted average of the stratum specific estimates.
Assuming equal weights:

What weights should we use? Based
on sample size in each stratum? Other
factors? More discussion on this later.
One more example of weighting; assumes 10 times the weight for stratum
1:
![]()
·
In addition to data-based criterion, 3 a priori
criteria.
·
Considered at study design stage to identify variables for possible
control in the analysis.
1. A confounder
must be a risk factor for the health outcome.
·
Example – relation between toxic chemical exposure and lung cancer
·
Based on the literature, may need to control for age and smoking status,
known risk factors for lung cancer.
·
The goal is to determine whether exposure to the chemical contributes
over and above the effects of age and smoking on lung cancer.
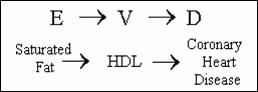
2. A confounder cannot be
an intervening variable between the exposure and the disease.
Example: Control for HDL?
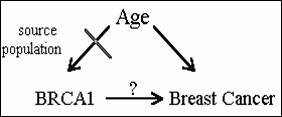
3. A confounder must be
associated with the exposure in the source population being studied.
Example: Case control study on genetic type BRCA1 and breast cancer; can
age confound the association? Assume no
association in source population between gene type and age; but a case-control
study finds an association. This would
be an example where criterion 3 is NOT met.
10-3 A
priori Criteria/Study Designs

Case-control study to assess relationship of alcohol consumption &
oral ca. 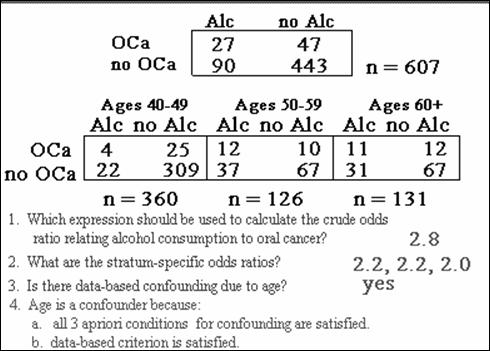
10-4 Confounding,
Interaction, and Effect Modification
Consider results from case-control study to assess relation between
alcohol consumption and bladder cancer. Data stratified on race (3 categories).
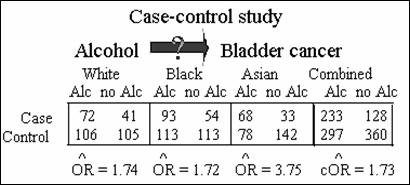
Note stratum-specific odds ratios.
Suggest interaction
Confounding? Precision-based OR = 2.16; little evidence of
confounding
Confounding and interaction are different concepts.
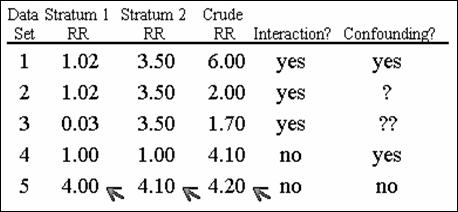
- Effect
modification often used interchangeably with term interaction.
·
A variable modifies the exposure-disease relationship.
·
A statistical test can be applied to determine the
presence/absence of interaction (e.g., Breslow-Day test)
·
A statistical test is not used for assessing confounding